Análisis de la segunda derivada.

El análisis de derivadas es una herramienta fundamental en matemáticas y en muchas ciencias

aplicadas. Al calcular derivadas, podemos estudiar el comportamiento de una función: dónde crece, dónde decrece, sus puntos de máximo y mínimo, entre otras características. La segunda derivada, en particular, nos permite determinar la concavidad de la función. Esto es clave en análisis de curvas, optimización y en estudios de fenómenos físicos y económicos. Una función es cóncava hacia arriba (o convexa) en un intervalo si la segunda derivada es positiva en ese intervalo, lo que implica que la curva tiene forma de "U". Por otro lado, una función es cóncava hacia abajo en un intervalo si la segunda derivada es negativa, lo cual produce una forma de

"N". A continuación, revisaremos dos ejercicios que ilustran cómo utilizar la segunda derivada para determinar la concavidad de una función.

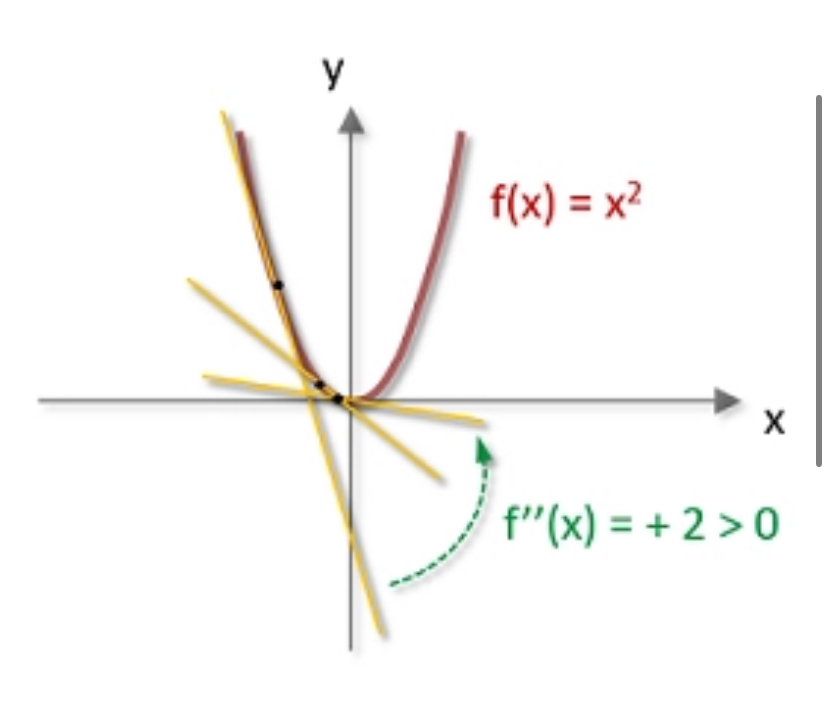
FUNCIÓN CÓNCAVA HACIA ARRIBA (CONVEXA)

Consideremos la función:

f(x) =x^2-4x+3

1. Primera Derivada: Calculamos la primera derivada de la función.

f'(x) = 2x -4

2. Segunda Derivada: Calculamos la segunda derivada para analizar la concavidad.

f"(x) = 2

3. Análisis de la Segunda Derivada:

Observamos que f"(x) = 2 es constante y positiva

para todo x, lo cual indica que la función es cóncava hacia arriba (convexa) en todo su dominio.

4. Conclusión: Como f"(x) > O para todos los valores de x, esto significa que la gráfica de f(x) = x^2-4x + 3 tiene una forma de "U" o "cuenco". La función es convexa, lo que implica que cualquier punto en el intervalo representa una curva que se abre hacia arriba.

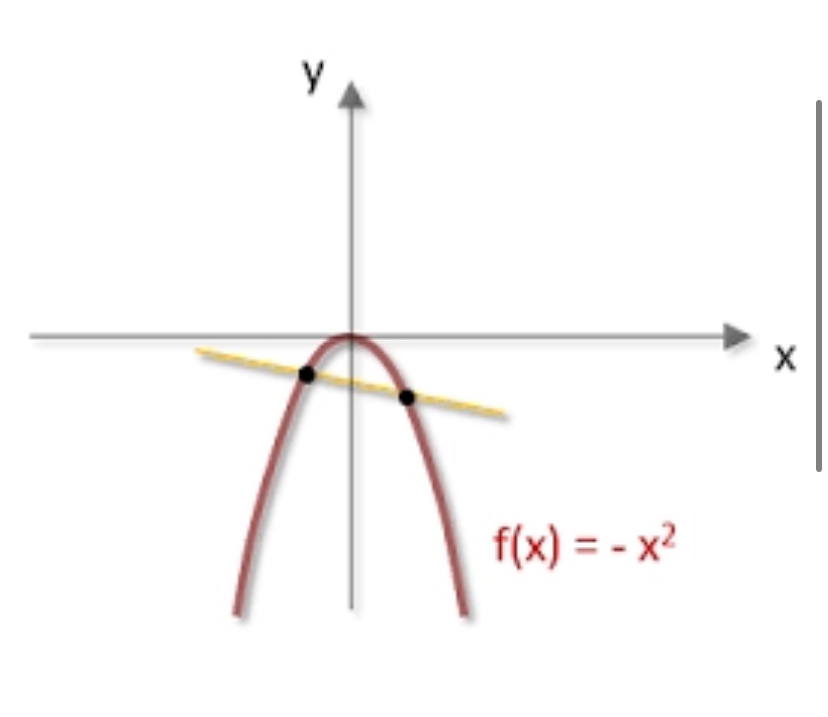
FUNCIÓN CÓNCAVA HACIA ABAJO

Ahora analicemos la función:

9(x) =-x^2+2x-1

1. Primera Derivada: Calculamos la primera derivada de la función.

g'(x)=-2x + 2

2. Segunda Derivada: Calculamos la segunda derivada para ver cómo afecta la concavidad.

9" (x) = -2

3. Análisis de la Segunda Derivada:

Notamos que g"(x) = -2, una constante negativa

para todo x, lo que implica que la función es cóncava hacia abajo en todo su dominio.

4. Conclusión: Dado que g"(x) < O para cualquier valor de x, la gráfica de g(x) = -x^2 + 2x - 1 tiene una forma de "N" o "techo invertido". La función es cóncava hacia abajo, lo que indica que todos los puntos de esta función caen en una curva que se abre hacia abajo.

PARA FINALIZAR MI COMCLUSION 

La segunda derivada es una herramienta poderosa para determinar si una función es cóncava hacia arriba o hacia abajo, proporcionando información valiosa sobre la forma de la curva. En los ejemplos anteriores, observamos que una segunda derivada positiva indica convexidad (cóncava hacia arriba), mientras que una segunda derivada negativa indica concavidad hacia abajo. Este análisis es fundamental en el cálculo y en aplicaciones de optimización y modelado en diversas áreas.